Bei Auswahl eines eisenlosen DC-Bürstenmotors für eine Anwendung oder bei Entwicklung eines angetriebenen Prototyps sind mehrere grundlegende motorphysikalische Prinzipien für die Auslegung eines sicheren, gut funktionierenden, und ausreichend dimensionierten Präzisionsantriebssystems zu berücksichtigen. In diesem Dokument haben wir einige wichtige Methoden, Formeln und Berechnungsdetails zusammengefasst, mit denen die Leistungsabgabe eines eisenlosen Motors, die Drehzahl-Drehmoment-Kennlinie des Motors und Strom- und Wirkungsgradkennlinien bestimmt werden können, sowie theoretische Berechnungen zur Abschätzung der Motorleistung eines kalten Motors.
Gleichstrommotoren sind Leistungswandler, denn sie wandeln elektrische Leistung (Pin) in mechanische Leistung (Pout) um. Der Quotient beider Terme entspricht dem Wirkungsgrad des Motors. Reibungs- und Kupferverluste zusammen ergeben den Leistungsverlust (Ploss) in Joule/s (Eisenverluste sind bei eisenlosen DC-Motoren vernachlässigbar). Bei Erwärmung des Motors ergeben sich zusätzliche Verluste, auf die wir weiter unten eingehen werden:
In der Physik ist die Leistung definiert als die in einem bestimmten Zeitraum eingesetzte Energie bezogen auf diesen Zeitraum. Die metrische Standardeinheit der Leistung ist das „Watt” W.
Wie wird die Leistung berechnet? Bei linearen Bewegungen ist die Leistung das Produkt aus Kraft und Weg pro Zeiteinheit P = F · (d/t). Da Geschwindigkeit der zurückgelegte Weg pro Zeiteinheit ist, ergibt sich P = F · s. Bei Drehbewegungen gilt daher analog, dass die Leistung das Produkt aus Drehmoment und Drehwinkel pro Zeiteinheit ist – oder einfach das Produkt aus Drehmoment und Winkelgeschwindigkeit.
Dabei gilt:
P = Leistung in W
M = Drehmoment in Nm
F = Kraft in N
d = Weg in m
t = Zeit in s
ω rad = Winkelgeschwindigkeit in rad/s
Als Symbol für das Drehmoment wird normalerweise der griechische Kleinbuchstabe “τ”(tau) oder manchmal auch nur der Buchstabe “T” verwendet. Wenn es jedoch als Kraftmoment bezeichnet wird, wird es üblicherweise mit dem Buchstaben “M” gekennzeichnet.
In der europäischen Nomenklatur wird oft der Kleinbuchstabe n” verwendet, um die Geschwindigkeit entlang einer Achse darzustellen. Gewöhnlich wird “n” in der Einheit Umdrehungen pro Minute oder U/min angegeben.
Bei der Berechnung der mechanischen Leistung ist es wichtig auf die Einheiten zu achten. Wenn „n“ (Geschwindigkeit) in min-1 angegeben ist, dann muss eine Umrechnung in die Einheit der Winkelgeschwindigkeit rad/s erfolgen. Dies erreicht man durch Multiplikation der Geschwindigkeit mit einem Umrechnungsfaktor von 2π/60. Ist „M“ (Drehmoment) in der Einheit mNm angegeben, dann muss eine Multiplikation mit 10-3 erfolgen (= Division durch 1 000), um die Einheit Nm für weitere Berechnungen zu erhalten.
Dabei gilt:
n = Drehzahl in min-1
M = Drehmoment in mNm
Als Beispiel soll die Leistung ermittelt werden, die der Motor 2668W024CR im kalten Zustand liefern muss, um ein Lastmoment von 68 mNm mit einer Drehzahl von 7 370 min-1 anzutreiben. Das Produkt aus Drehmoment, Drehzahl und dem entsprechenden Umrechnungsfaktor ist unten dargestellt.
Die Berechnung der benötigten Antriebsleistung ist oft der erste Schritt bei der Auswahl von Motoren oder Getriebemotoren. Ist die benötigte mechanische Ausgangsleistung für eine vorgegebene Anwendung bekannt, können die Leistungsdaten für Maximal- und Dauerleistung verschiedener Motoren verglichen werden, um festzustellen, welche Motoren für den Einsatz in der Anwendung infrage kommen.
Am Beispiel des eisenlosen Gleichstrommotors 2668W024CR stellen wir im Folgenden eine Methode zur Bestimmung der Motorparameter vor. Zuerst erläutern wir einen eher empirischen Ansatz, dann führen wir eine theoretische Berechnung durch.
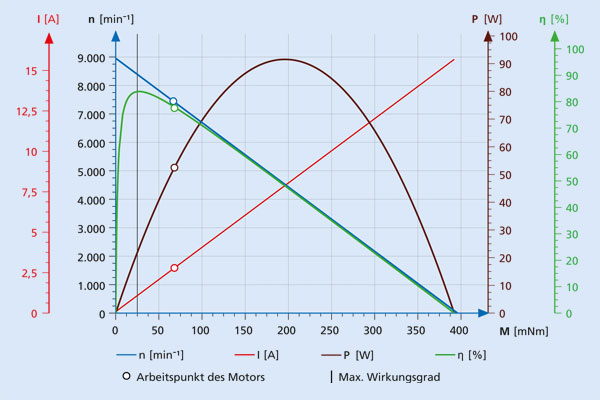
Zur grafischen Darstellung von Motorkennlinien verwendet man häufig Drehzahl-Drehmoment-Kennlinien. Obwohl Drehzahl-Drehmoment-Kennlinien in der Fachliteratur üblicherweise für größere Gleichstrommaschinen verwendet werden, kann man sie auch bei kleinen, eisenlosen Motoren anwenden.
In Drehzahl-Drehmoment-Kennlinien werden Motordrehzahl, Motorstrom, mechanische Ausgangsleistung und Wirkungsgrad als Funktionen des Motordrehmoments dargestellt. Im Folgenden beschreiben wir, wie man aus einer Reihe von Rohdatenmessungen zu einem Satz von Drehzahl-Drehmoment-Kennlinien für einen typischen Gleichstrommotor gelangt.
Der 2668W024CR hat eine Nennspannung von 24 V. Mit ein paar Basis-Laborgeräten können Sie an einem eisenlosen Gleichstrommotor der Serie 2668 CR die Drehzahl-Drehmoment-Kennlinien an einem bestimmten Betriebspunkt messen.
Viele Parameter können direkt über einen Motion Controller, wie z.B. einen MC3 Motion Controller von FAULHABER, ermittelt werden. Die meisten Controller-Hersteller bieten Software an, wie z.B. den FAULHABER Motion Manager, der mit einer Trace-Funktion Spannung, Strom, Position, Geschwindigkeit usw. aufzeichnet. Sie können auch exakte Momentaufnahmen des Motorbetriebs bis ins kleinste Detail liefern. Die Motion-Controller der MC3-Familie (MC 5004, MC 5005 und MC 5010) können z.B. alle eine Vielzahl von Bewegungsparametern messen. Zur Erfassung der Daten für eine Drehzahl-Drehmoment-Kennlinie ist das wahrscheinlich der schnellste Weg, aber nicht der einzige.
Steht kein Controller mit Trace-Funktion zur Verfügung, kann man auch mit Basis-Laborgeräten die Kenndaten eines Motors beim Blockieren, im Leerlauf und bei Nennlast ermitteln. Betreiben Sie den 2668W024CR ohne Last mit einem auf 24 V eingestellten Labornetzteil und messen Sie die Drehzahl kontaktlos (z.B. mit einem Stroboskop). Messen Sie ebenfalls den Motorstrom im Leerlauf. Eine Strommesszange ist für diese Messung ideal, da damit kein zusätzlicher Reihenwiderstand zum Motor im Betrieb hinzugeschaltet werden muss. Mit einer kleinen Pulverbremse oder einer Hysterese-Leistungsbremse, kann eine einstellbaren Last an die Motorwelle gekoppelt werden.
Erhöhen Sie nun das Motordrehmoment so weit bis der Motor stehen bleibt. Messen Sie im Stillstand das Drehmoment der Bremse und den Motorstrom. Um die Berechnung zu vereinfachen, gehen wir davon aus, dass die Bremsenankopplung keine zusätzliche Last für den Motor darstellt und dass die Belastung durch die Bremse keine unbekannten Reibungsanteile enthält. Es ist jetzt auch sinnvoll, den Anschlusswiderstand des Motors zu messen. Schließen Sie ein Ohmmeter an die Motorklemmen an, um den Widerstand zu messen. Drehen Sie die Motorwelle und nehmen Sie eine weitere Messung vor. Die Messwerte sollten sehr nahe beieinander liegen. Drehen Sie die Welle weiter und nehmen Sie mindestens drei Messungen vor. Dadurch stellen Sie sicher, dass Sie die Messungen nicht an einem Punkt mit minimalem Kontakt am Kommutator vorgenommen haben.
Bislang haben wir gemessen:
n0 = Leerlaufdrehzahl
I0 = Leerlaufstrom
MH = Anhaltemoment
R = Anschlusswiderstand
Sie können ein Diagramm vorbereiten, bei dem das Motordrehmoment auf der Abszisse (horizontale Achse),die Geschwindigkeit auf der linken Ordinate (vertikale Achse) und der Strom auf der rechten Ordinate dargestellt werden. Skalieren Sie die Achsen basierend auf den Messungen, die Sie in Schritt eins vorgenommen haben. Ziehen Sie eine gerade Linie vom linken Ursprung des Diagramms (Drehmoment und Strom = 0) zum Haltestrom auf der rechten Ordinate (Anhaltemoment und Haltestrom). Diese Linie stellt den Motorstrom in Abhängigkeit vom Motordrehmoment dar. Die Steigung dieser Linie ist die Stromkonstante kI, die als Proportionalitätskonstante das Verhältnis zwischen Motorstrom und Motordrehmoment angibt (in der Einheit Strom pro Drehmoment oder A/mNm). Der Kehrwert dieser Steigung ist die Drehmomentkonstante kM (in der Einheit Drehmoment pro Strom oder mNm/A).
Dabei gilt:
kI = Stromkonstante
kM= Drehmomentkonstante
Vereinfachend nehmen wir an, dass der Motor keine innere Reibung hat. In der Praxis bestimmt man das Reibungsmoment des Motors MR durch Multiplikation der Drehmomentkonstante kM odes Motors mit dem gemessenen Leerlaufstrom I0. Unter Berücksichtigung des Reibungsmoments beginnen die Drehzahl-Drehmoment-Kennlinie und die Drehmoment-Strom-Kennlinie dann nicht an der linken vertikalen Achse, sondern mit einem Versatz auf der horizontalen Achse, der dem berechneten Reibungsmoment entspricht.
Meistens kann man einfach zwei zusätzliche vertikale Achsen hinzufügen, um Leistung und Wirkungsgrad als Funktionen des Drehmoments darzustellen. Eine zweite vertikale Achse wird normalerweise für den Wirkungsgrad und eine dritte vertikale Achse für die Leistung verwendet. Zur Vereinfachung stellen wir die Wirkungsgrad-Drehmoment- und Leistungs-Drehmoment-Kennlinien im gleichen Diagramm dar wie die Drehzahl-Drehmoment- und Strom-Drehmoment-Kennlinien (siehe Beispiel unten).
Erstellen Sie eine Tabelle, in der Sie die mechanische Motorleistung an verschiedenen Betriebspunkten eintragen – vom Leerlauf bis zum Anhaltemoment. Da die mechanische Ausgangsleistung einfach das Produkt aus Drehmoment und Drehzahl mit einem Korrekturfaktor für die Einheiten ist (siehe Abschnitt über die Berechnung der benötigten Antriebsleistung), kann die Leistung unter Verwendung der zuvor eingezeichneten Drehzahl-Drehmoment-Kennlinie berechnet werden.
Tabelle 1 zeigt eine Beispiel-Berechnungstabelle für den Motor 2668W024CR. Jeder berechnete Punkt für die Leistung wird dann grafisch dargestellt. Die resultierende Funktion ist eine parabolische Kurve, wie unten in Grafik 1 dargestellt. Die maximale mechanische Leistung ergibt sich bei etwa der Hälfte des Anhaltemoments. Die Drehzahl an diesem Punkt entspricht in etwa der halben Leerlaufdrehzahl.
Erstellen Sie eine Tabelle, in der Sie den Motorwirkungsgrad an verschiedenen Betriebspunkten eintragen – vom Leerlauf bis zum Anhaltemoment. Die an den Motor angelegte Spannung ist bekannt, und die Strom-Drehmoment-Kennlinie wurde eingezeichnet. Das Produkt aus Motorstrom und angelegter Spannung entspricht der Leistungsaufnahme des Motors. An jedem zu berechnenden Punkt ist der Wirkungsgrad η des Motors gleich der abgegebenen mechanischen Leistung geteilt durch die aufgenommene elektrische Leistung. Auch hierfür findet man in der Beispieltabelle für den Motor 2668W024CR (Tabelle 1) entsprechende Werte und eine Beispielkurve in Grafik 1. Der maximale Wirkungsgrad ergibt sich bei etwa 10% des Motor-Anhaltemoments.
Kennlinien-Definitionen
Motorkennlinien
| Laststrom | 2,79 A |
| Spannung | 24,11 V |
| Motorwicklungstemperatur | 140,23 °C |
| Motorgehäusetemperatur | 105,03 °C |
| Erforderliche Motordrehzahl | 7370 min-1 |
| Benötigtes Lastmoment | 68 mNm |
| Abgabeleistung | 52,48 W |
| Wirkungsgrad (gesamt) | 77,97 % |
Hinweis: Aus Platzgründen wird nur eine Beispielberechnung für einen Punkt angezeigt.
Ein weiterer hilfreicher Parameter bei der Motorauslegung ist die Motorkonstante. Die richtige Nutzung dieser Kennzahl kann den iterativen Prozess bei der Auswahl eines Gleichstrommotors erheblich abkürzen. Sie beschreibt einfach gesagt das Vermögen eines Wandlers, elektrische Leistung in mechanische umzuwandeln.
Der maximale Wirkungsgrad ergibt sich bei etwa 10% des Motor-Anhaltemoments. Der Nenner beschreibt den widerstandsbedingten Leistungsverlust. Mit ein paar Umrechnungen kann man die Gleichung vereinfachen:
Denken Sie daran, km (Motorkonstante) nicht mit kM (Drehmomentkonstante) zu verwechseln. Bei der Motorkonstante ist das tiefgestellte Zeichen „m“ ein Kleinbuchstabe, während bei der Drehmomentkonstante „M“ ein Großbuchstabe verwendet wird.
Für einen bürstenbehafteten oder bürstenlosen Gleichstrommotor relativ geringer Größe kann man die Beziehungen, die das Verhalten des Motors unter verschiedenen Umständen bestimmen, aus den Gesetzen der Physik und den Eigenschaften der Motoren selbst ableiten. Das 2. Kirchoffsche Gesetz besagt: „Alle Teilspannungen eines Umlaufs in einem elektrischen Netzwerk addieren sich zu null.“ Bei einem Gleichstrommotor, der mit einer Gleichspannungsquelle in Reihe geschaltet ist, kann das 2. Kirchoffsche Gesetz wie folgt ausgedrückt werden: „Die Nennspannung des Netzteils muss der Summe des Spannungsabfälle über den Wicklungswiderstand und der vom Motor erzeugten Gegen-EMK entsprechen.“
Normalerweise geben Motorhersteller die Gegen-EMK- Konstante des Motors in V/min-1 oder mV/min-1 an. Um einen sinnvollen Wert für die Gegen-EMK zu erhalten, muss man die Motorgeschwindigkeit in Einheiten angeben, die zur angegebenen Gegen-EMK-Konstante kompatibel sind.
„Alle Teilspannungen eines Umlaufs in einem elektrischen Netzwerk addieren sich zu null.“
(2. Kirchoffsches Gesetz)
Die Motorkonstante hängt von Spulenkonstruktion und Stärke und Richtung der Flusslinien im Luftspalt ab. Auch wenn man zeigen kann, dass die drei normalerweise angegebenen Motorkonstanten (Gegen-EMK-Konstante, Drehmomentkonstante und Drehzahlkonstante) bei Verwendung der korrekten Einheiten gleich sind, wird die Berechnung durch die Angabe der drei Konstanten in den allgemein akzeptierten Einheiten erleichtert.
Das vom Rotor erzeugte Drehmoment ist direkt proportional zum Strom in den Rotorwicklungen. Die Proportionalitätskonstante ist die Drehmomentkonstante des Motors.
Dabei gilt:
MR= Reibungsmoment des Motors
ML = Lastmoment
Unter der Annahme, dass eine konstante Spannung an den Motorklemmen anliegt, ist die Motorgeschwindigkeit direkt proportional zur Summe aus Reibungsmoment und Lastmoment. Die Proportionalitätkonstante entspricht der Neigung der Drehzahl-Drehmoment-Kennlinie. Bei geringer Neigung ist die Motorleistung besser. Je steiler die Kennlinie abfällt, desto schlechter ist die Motorleistung, die man von einem bestimmten eisenlosen Motor erwarten kann. Dieses Verhältnis kann man wie folgt berechnen:
Lassen Sie uns ein wenig in die theoretischen Berechnungen einsteigen. Der eisenlose Gleichstrommotor 2668W024CR soll mit 24 V an den Motorklemmen und einem Lastmoment von 68 mNm betrieben werden. Dazu muss die resultierende Motorkonstante, die Motordrehzahl, der Motorstrom, der Motorwirkungsgrad und die Ausgangsleistung ermittelt werden. Dem Motordatenblatt kann man entnehmen, dass die Leerlaufdrehzahl des Motors 7 800 min-1 bei 24 V beträgt. Ohne Last an der Motorwelle würde der Motor mit dieser Drehzahl laufen.
Einen ersten Eindruck von der Motorleistung gewinnen wir durch die Berechnung der Motorkonstante km. In diesem Fall ergibt sich eine Konstante von 28,48 mNm/A. „Der elektrische Widerstand liegt nach Datenblatt des Motors bei 1,03 Ohm im kalten Zustand für die 24V-Variante.“
Die Motordrehzahl unter Last ergibt sich aus der Leerlaufdrehzahl abzüglich der Drehzahlverminderung durch die Last. Die Proportionalitätskonstante für die Beziehung zwischen Motordrehzahl und Motordrehmoment ist die Steigung der Drehzahl-Drehmoment-Kennlinie, die sich aus Leerlaufdrehzahl des Motors geteilt durch das Anhaltemoment ergibt. In diesem Beispiel berechnen wir die Drehzahlverminderung (unter Vernachlässigung von Temperatureffekten), die durch die Drehmomentbelastung von 68 mNm verursacht wird, durch Herausrechnen der mNm-Einheiten:
Der Motorstrom unter Last ist die Summe aus Leerlaufstrom und dem aus der Last resultierenden Strom.
Die Drehmomentkonstante (kM) stellt die Beziehung zwischen Strom und Drehmoment dar. Dieser Wert beträgt 28,9 mNm/A. Nimmt man den Kehrwert, so erhält man die Stromkonstante kI, mit der man den Strom unter Last berechnen kann. In diesem Fall beträgt die Last 68 mNm, und der aus dieser Last resultierende Strom (unter Vernachlässigung von Temperatureffekten) beträgt ungefähr:
Ein Strom I, der durch einen Widerstand R fließt, führt zu einem Leistungsverlust I2 · R in Form von Wärme. Bei einem Gleichstrommotor ergibt das Produkt aus dem Quadrat des Motorstroms und Wicklungswiderstand die Verlustleistung als Wärme in den Rotorwicklungen. Bei einem Motorstrom von 0,203 A und einem Wicklungswiderstand von 14,5 Ω, geht folgende Leistung als Wärme in den Wicklungen verloren:
Die durch die Verluste I2 · R entstehende Wärme wird über die Motorkomponenten und den Luftstrom im Luftspalt abgeleitet. Der Wärmewiderstand ist ein Maß dafür, wie effizient Wärme von einem Motor (oder einem anderen System) abgeleitet werden kann.
Der Wärmewiderstand (der Kehrwert der Wärmeleitfähigkeit) gibt an, wie gut ein Material der Wärmeübertragung über einen definierten Weg widersteht. Motorhersteller geben üblicherweise mit Angabe des Wärmewiderstands Rth einen Hinweis auf die Fähigkeit des Motors, Wärme abzuleiten; z.B. hat eine Aluminiumplatte mit großem Querschnitt einen sehr geringen Wärmewiderstand, während die Werte für Luft oder Vakuum wesentlich höher liegen. Bei Gleichstrommotoren gibt es einen thermischen Pfad von den Motorwicklungen zum Motorgehäuse und einen zweiten thermischen Pfad zwischen Motorgehäuse und Motorumgebung (Umgebungsluft usw.). Einige Motorenhersteller geben für jeden der beiden thermischen Pfade einen Wärmewiderstand an, während andere nur die Summe der beiden als Gesamt-Wärmewiderstand des Motors angeben. Wärmewiderstandswerte werden in der Einheit Temperaturerhöhung pro Verlustleistung angegeben. Der Gesamtverlust I2 · R in den Wicklungen (der Wärmequelle) wird mit den thermischen Widerständen multipliziert, um die Wicklungstemperatur im Betrieb zu bestimmen. Der Temperaturerhöhung des Motors im Betrieb (T) beträgt:
Dabei gilt:
ΔT = Temperaturanstieg in K
I = Strom durch die Motorwicklungen in A
R = Widerstand der Motorwicklungen in Ω
Rth1 = Wärmewiderstand zwischen Wicklungen und Gehäuse in K/W
Rth2 = Wärmewiderstand zwischen Gehäuse und Umgebung in K/W
Setzen wir unser Beispiel mit dem Motor 2668W024CR mit folgenden Betriebswerten fort: Strom von 2,458 A in den Motorwicklungen, Wicklungswiderstand von 1,03 Ω, Wärmewiderstand Wicklung zu Gehäuse von 3 K/W und Wärmewiderstand Gehäuse zu Umgebung von 8 K/W. Der Temperaturanstieg der Wicklungen wird mit folgender Formel berechnet; Ploss kann man durch I2 · R ersetzen:
Da die Einheitenabstufung bei Kelvin-Skala und Celsius-Skala gleich ist, können wir den Kelvin-Wert einfach durch den Celsius-Wert ersetzen. Bei einer Umgebungslufttemperatur von 22°C kann die reale Betriebstemperatur der Motorwicklungen wie folgt abgeschätzt werden:
Es muss sichergestellt werden, dass die reale Betriebstemperatur der Wicklungen den auf dem Datenblatt angegebenen Bemessungswert des Motors nicht überschreitet. Im obigen Beispiel beträgt die maximal zulässige Wicklungstemperatur 125°C. Da die berechnete Betriebstemperatur der Wicklungen nur bei 90,4°C liegt, sollten thermische Schäden an den Motorwicklungen bei dieser Anwendung nicht auftreten.
Mit ähnlichen Berechnungen kann man andere Fragen beantworten. Beispielsweise kann es für eine Anwendung erforderlich sein, dass ein Motor dauerhaft bei seinem maximalen Drehmoment betrieben wird und man hofft, dass keine Schäden durch Überhitzung auftreten. Angenommen, ein Motor soll mit dem maximal möglichen Drehmoment bei einer Umgebungslufttemperatur von 22°C betrieben werden. Der Konstrukteur möchte wissen, welches Drehmoment der Motor ohne Überhitzung sicher bereitstellen kann. Auch gibt das Datenblatt für den eisenlosen Motor 2668W024CR eine maximale Wicklungstemperatur von 125°C an. Bei einer Umgebungstemperatur von 22°C, kann der folgende maximale Temperaturanstieg des Rotors toleriert werden: 125°C – 22°C = 103°C
Damit können wir den Anstieg des Wicklungswiderstands aufgrund der thermischen Verluste berechnen:
Aufgrund der thermischen Verlustleistung I2 · R lund der damit einhergehenden Erwärmung von Wicklung und Magnet steigt der Wicklungswiderstand von 1,03 Ω auf 1,44 Ω. Mit diesem Wert können wir die Drehmomentkonstante kM neu berechnen, um die Auswirkungen des Temperaturanstiegs auf die Motorleistung zu ermitteln:
Wie wir sehen können, schwächt sich die Drehmomentkonstante genau wie die Gegen-EMK-Konstante durch die Temperaturerhöhung ab! Der Wicklungswiderstand des Motors, Drehmomentkonstante und Gegen-EMK-Konstante werden also negativ beeinflusst, und zwar aus dem sehr einfachen Grund, dass sie alle Funktionen der Temperatur sind.
Wir könnten weitere Parameter berechnen, um das Ergebnis von wärmerer Wicklung und Magnet zu berücksichtigen, aber optimale Ergebnisse erzielt man iterativ, was am besten mit mathematischer Software gelingt. Steigende Motortemperatur verändert jeden der drei Parameter in einer Weise, die die Motorleistung verschlechtert und die Leistungsverluste erhöht. Im Dauerbetrieb könnte ein Motor sogar thermisch instabil und damit irreparabel beschädigt werden. Dies kann selbst dann geschehen, wenn erste Berechnungen einen akzeptablen Temperaturanstieg ergeben (mit Werten von R und kM bei Umgebungstemperatur).
Beachten Sie, dass man durch Verringerung des Wärmewiderstands des Motors den maximal zulässigen Strom durch die Motorwicklungen erhöhen kann. Der Wärmewiderstand zwischen Rotor und Gehäuse Rth1 wird in erster Linie durch die Motorkonstruktion bestimmt. Der Wärmewiderstand zwischen Gehäuse und Umgebung Rth2 kann durch den Einbau von Kühlkörpern deutlich verringert werden. Bei der Angabe von Wärmewiderständen für kleine Gleichstrommotoren wird angenommen, dass der Motor komplett von Luft umgeben ist. Alleine der Einbau des Motors in einen wärmeleitenden Rahmen oder Chassis ist daher schon eine Art von Kühlkörper. Einige Hersteller von größeren Gleichstrommotoren geben den Wärmewiderstand für die Montage des Motors auf einer Metallplatte mit bekannten Abmessungen und Material an.
Für weitere Informationen zu Berechnung von eisenlosen DC-Bürstenmotoren und Beeinträchtigung der Leistung von Elektromotoren durch Wärmeverluste wenden Sie sich bitte an einen qualifizierten FAULHABER Applikationsingenieur. Wir helfen Ihnen gerne.